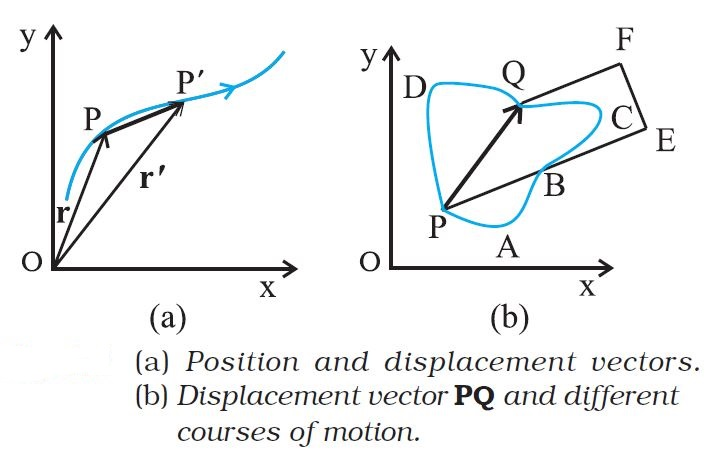
In physics, we can classify quantities as scalars or vectors. Basically, the difference is that a direction is associated with a vector but not with a scalar.
`\color{fuchsia} \mathbf\ul"SCALAR QUANTITY"`
`\color{purple} "★ DEFINITION ALERT"`
`\color{purple} ✍️` A scalar quantity is a quantity with magnitude only. It is specified completely by a single number, along with the proper unit.
`\color{green}"Examples"` - Distance, Mass, Temperature, Volume etc.
`\color{green} ★ \color{green} \mathbf(KEY \ CONCEPT)`
`\color{green} ✍️` Scalars can be added, subtracted, multiplied and divided just as the ordinary numbers. (Rules of ordinary algebra)
`\color{green} ✍️` Addition and subtraction of scalars make sense only for quantities with same units. However, you can multiply and divide scalars of different units.
`\color{fuchsia} \mathbf\ultext(VECTOR QUANTITY)`
`\color{purple} "★ DEFINITION ALERT"`
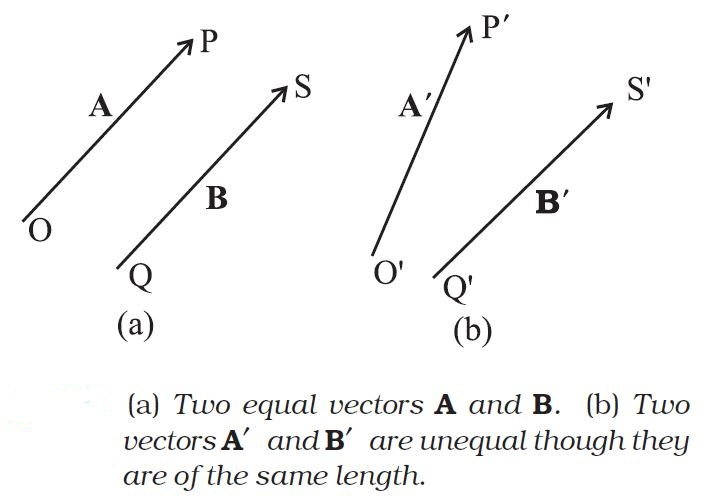
`\color{purple} ✍️` A vector quantity is a quantity that has both a magnitude and a direction and obeys the `text(triangle law of addition)` or equivalently the `text(parallelogram law of addition)`. So, a vector is specified by giving its magnitude by a number and its direction.
`\color{green}"Examples"` - Displacement, Velocity, Acceleration, Force, etc.
`\color{green} ★ \color{green} \mathbf(KEY \ CONCEPT)`
`\color{green} ✍️` To represent a vector, we use an arrow placed over a letter, say `vecv`.
`\color{green} ✍️` The magnitude of a vector is often called its absolute value, indicated by `|vecv| = v`
In physics, we can classify quantities as scalars or vectors. Basically, the difference is that a direction is associated with a vector but not with a scalar.
`\color{fuchsia} \mathbf\ul"SCALAR QUANTITY"`
`\color{purple} "★ DEFINITION ALERT"`
`\color{purple} ✍️` A scalar quantity is a quantity with magnitude only. It is specified completely by a single number, along with the proper unit.
`\color{green}"Examples"` - Distance, Mass, Temperature, Volume etc.
`\color{green} ★ \color{green} \mathbf(KEY \ CONCEPT)`
`\color{green} ✍️` Scalars can be added, subtracted, multiplied and divided just as the ordinary numbers. (Rules of ordinary algebra)
`\color{green} ✍️` Addition and subtraction of scalars make sense only for quantities with same units. However, you can multiply and divide scalars of different units.
`\color{fuchsia} \mathbf\ultext(VECTOR QUANTITY)`
`\color{purple} "★ DEFINITION ALERT"`
`\color{purple} ✍️` A vector quantity is a quantity that has both a magnitude and a direction and obeys the `text(triangle law of addition)` or equivalently the `text(parallelogram law of addition)`. So, a vector is specified by giving its magnitude by a number and its direction.
`\color{green}"Examples"` - Displacement, Velocity, Acceleration, Force, etc.
`\color{green} ★ \color{green} \mathbf(KEY \ CONCEPT)`
`\color{green} ✍️` To represent a vector, we use an arrow placed over a letter, say `vecv`.
`\color{green} ✍️` The magnitude of a vector is often called its absolute value, indicated by `|vecv| = v`